Datatypes¶

Icon is rich in datatypes. Unicon is just that much richer.

Immutable Unicon Datatypes¶

Unicon starts out with some immutable types:

Integer (arbitrary size)
floating point Real numbers
String
Cset (sets of characters - ASCII)

Note: string is an immutable type. New strings will be formed for operations that look like they are modifying a string in place. This has consequences, detailed in the String entry.

Integer¶

Integers in Unicon can be any size, (when the large integers feature is compiled in) and are always exact values.

Radix prefix¶

Integer literals in source code can be of any base from 2 through 36, by using a radix prefix; the default being decimal, base 10. The radix is always a decimal number, followed by the letter r or R followed by digits of the value.

The above, are all valid literals for the value forty-two. Base 0 and base 1 are invalid, and will produce a compile time error

#
# Numeric literals, with errors
#
procedure main()
    write("Various forms of the ultimate answer")
    write(42)
    write(2r101010)
    write(5r132)
    write(16r2A)
    write(16R2a)
    write(36r16)

    write(0r42)
    write(1r42)
end

examples/numeric-literals-errors.icn

Sample run (with errors):

prompt$ unicon -s numeric-literals-errors.icn -x
File numeric-literals-errors.icn; Line 20 # invalid radix for integer literal
File numeric-literals-errors.icn; Line 20 # invalid integer literal
numeric-literals-errors.icn:20: # "42": syntax error (104;258)
File numeric-literals-errors.icn; Line 21 # invalid radix for integer literal
File numeric-literals-errors.icn; Line 21 # invalid integer literal
numeric-literals-errors.icn:21: # "42": syntax error (104;258)

Getting rid of the troublesome lines (and adding some larger numbers):

#
# Numeric literals
#
procedure main()
    write("Various forms of the ultimate answer")
    write(42)
    write(2r101010)
    write(5r132)
    write(16r2A)
    write(16R2a)
    write(36r16)

    ## illegal radix   write(0r42)
    ## illegal radix   write(1r42)

    write("And now some larger values")
    write(36r16K)
    write(36r0to9andAtoZ)
end

examples/numeric-literals.icn

Sample run:

prompt$ unicon -s numeric-literals.icn -x
Various forms of the ultimate answer
42
42
42
42
42
42
And now some larger values
1532
3013673839525331

Base radix also influences the digits allowed in the value. For base eight, 8 and 9 are illegal, not being part of the valid set of digit symbols. For base two, only 0 and 1 are allowed. For bases above ten, the alphabet is used. A (or a) represents ten, B/b is eleven, Z/z represents thirty-five with radix 36.

Given

write(3r42)

unicon will report a syntax error

File numbers.icn; Line 16 # invalid integer literal
numbers.icn:16: # "42": syntax error (104;258)

Case sensitivity¶

Unlike most of Unicon (being case sensitive), the Radix indicator R is case insensitive, R and r both work. As do upper and lower case letters when used as digits. 2A and 2a are both valid representations of forty-two in hexadecimal (assuming the 16r radix is given first). All of 16R2a, 16R2A, 16r2a and 16r2A represent 42 in base 10.

Octal¶

Unicon does NOT follow the C convention of 0 prefixed literals being treated as octal (base eight), values. Use 8r0777 if you feel the need to prefix your octal constants with a zero. 8r777 will work just as well for representing five hundred eleven. 042 is forty two, not thirty four as a Unicon numeric literal, unlike C and some other languages.

~= 34

== 42

== 8r52

Scaling suffix¶

And just to add to the flexibility, Unicon supports a trailing suffix that closely resembles the International System of Units SI standard, but scaled for binary computers and not the normal decimal base in thousands. Unicon uses 1024 based scaling.

K (or k) kilo, literal is multiplied by $1024$
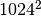
M (or m) mega, literal is multiplied by $1024^2$
G (or g) giga, $1024^3$
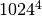
T (or t) tera, $1024^4$
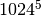
P (or p) peta, $1024^5$

write(42)
write(42K)
write(42M)
write(42g)
write(42t)
write(42P)

Gives

42
43008
44040192
45097156608
46179488366592
47287796087390208

To make for some sanity, the suffixes are only supported for decimal (base ten) literals. Even considering the scaling is actually a binary and not decimal thousands based scaling. For instance 36r16K is a base 36 literal of the value 16K (1532 decimal), not 36r16 modified by a suffix K.

The scaling suffixes are also case insensitive.

Positive and negative¶

The + (plus) and - (minus) signs can be used with any of these literals, and come before any radix specifier.

-2r101010 == -42
-16r2A    == -42
-16R2a    == -42
+36r16    == +42

There is no such thing as a negative base in Unicon so the sign always effects the value, never the radix (or the meaning of the scaling suffix).

Arbitrary magnitude¶

One of the nicer things with Unicon is the unlimited integer size.

n := 123456789012345678901234567890123456789012345678901234T
write(n)

Gives that long literal (scaled by tera, T, 1024^4), which displays as

135742175046962388768696238876869623887686962388768695614475075584

Unicon Integer data is always exact, regardless of magnitude. Unless you run out of memory, or other error condition has been triggered.

Play nice¶

Given all that flexibility, do yourself, and everyone else, a favour and stick with literals that conceptually make sense for the task at hand. Don’t use base thirteen literals, just because you can. Stick with the ten fingers for most code, and go to another radix only when it makes sense. Use 8r octal numbers when dealing with things like Unix permissions, or 2r for bit patterns. Base twenty-three literals will just cause confusion, for no reason and slow down everyone that wants to read through your program sources. Using unicon is proof enough that you are smart cookie.

Real numbers¶

Unicon also supports double precision floating point real numbers (in base ten, decimal).

+/- digits, a decimal point (period), more digits, optional +/- E exponent

write(1.23)
write(.23)
write(1.)
write(1.23E42)
write(-1.23E-42)

Floating point is an inexact science. The internal representation is an approximation brought on by differences between binary and decimal notation.

0.5, is exact, both in decimal and base two arithmetic. But many values, such as 0.3 can cause problems when scaled, multiplied and divided. Be wary of precisions, rounding errors and keep a healthy skepticism when dealing with floating point double precision values.

Don’t rely on floating point math for financial calculations. Use fixed point integer math or use something like GnuCOBOL for problems that require bank safe computations.

Having said that, there is science behind floating point representation and for most engineering problems, close enough, is usually a realistic expectation.

Floating point coercion¶

Unicon will always attempt to match integer and floating point calculations, promoting values to and from integer and real as hinted at by the code and the datatypes forming the computation.

write("Integer division")
every i := 1 to 8 do write(2 / i)

write()

write("Real division")
every i := 1 to 8 do write(2.0 / i)

Gives two completely different sets of output. The first every loop uses integer division, fractions lost and mostly zeros. The second uses floating point math, the 2.0 literal forcing the floating point computation, and a Real result:

prompt$ unicon numbers.icn -x

Integer division
2
1
0
0
0
0
0
0

Real division
2.0
1.0
0.6666666666666666
0.5
0.4
0.3333333333333333
0.2857142857142857
0.25

Any Real value in a computational input will cause a Real result. When all the input values are Integer, the result is Integer, even if it seems like it should cause a fractional answer.

String to number coercion¶

Unicon will do similar implicit coercion of data types when given a String value as part of a numerical equation. If a String can safely be converted to a numeric value, Integer or Real, it will be. If not, it will raise a run-time error.

write("String as Integer division")
every i := 1 to 4 do write("2"/i)
write()

write("String as Real division")
every i := 1 to 4 do write("2.0"/i)
write()

write("String as garbage division")
every i := 1 to 4 do write("2.o"/i)

Gives:

String as Integer division
2
1
0
0

String as Real division
2.0
1.0
0.6666666666666666
0.5

String as garbage division

Run-time error 102
File numbers.icn; Line 40
numeric expected
offending value: "2.o"
Traceback:
   main()
   {"2.o" / 1} from line 40 in numbers.icn

Explicit type conversions¶

Conversion of data types can also be explicit.

write("String as explict Real division")
every i := 1 to 4 do write(real("2")/i)

Produces:

String as explicit Real division
0
0
6666666666666666
5

The built-in functions real(s) and integer(s) can be used to convert String, Real and Integer data to the given numeric form.

integer(r) will be a truncation conversion. integer(2.3) and integer(2.9) both return 2. real(i) may lose precision once the integer value exceeds what can be stored in a floating point double precision value.

n := 123456789012345678901234567890123456789012345678901234
write(n)
write(real(n))
write(integer(real(n)))

Shows as

123456789012345678901234567890123456789012345678901234
1.234567890123457e+53
123456789012345677902421375322642595439917720609488896

A huge loss of precision occurs after 16 digits of decimal. Don’t be firing any NASA spacecraft out toward Jupiter without very careful consideration of floating point Real number precision and accuracy. Unicon is not at fault here, it is in the nature of approximation with floating point representations.

Again, in most day to day real world operations, unless you are trying to fire a rocket with sub-nanometre accuracy across a trillion kilometre distance, Unicon Real values will be close enough. For pure mathematics? Not even in the same ball park.

Cset¶

A character set. A highly efficient datatype for pattern matching.

Csets are limited to single byte values, 0 through 255. There are no duplicates within a Cset. Cset literals use single quotes in Unicon.

#
# cset-samples.icn, demonstrate some Csets
#
procedure main()
    noDupes := 'hello'
    write("Given 'hello': ", noDupes, " ", image(noDupes))
    
    cs := 'abcdef'
    write(cs, " ", image(cs))

    complement := ~cs
    write("Size of complement of ", image(cs), ": ", *complement)

    write("Size of complement of &letters: ", *~&letters)
end

examples/cset-samples.icn

Sample run:

prompt$ unicon -s cset-samples.icn -x
Given 'hello': ehlo 'ehlo'
abcdef 'abcdef'
Size of complement of 'abcdef': 250
Size of complement of &letters: 204

String¶

This, is where Unicon shines. String manipulation is at the heart and soul of Icon, Unicon, and back all the way to SNOBOL. Pattern matching, string scanning, slicing, dicing and transformation operations you probably haven’t even thought of yet. All nicely packaged in the Unicon executable, very clearly, and very concisely. Ralph Griswold was one of those genius level computer scientists, who led the core Icon developers to exceed expectations and go above and beyond the norm. Clint Jeffery and his team are now pushing those expectations out even further with Unicon. Release 13 of Unicon has SNOBOL inspired pattern matching operations built in, a huge testament to the legacy and future of Unicon programming. More on that in the SNOBOL patterns chapter.

In Unicon, String data is immutable, and is never changed in place. New String data is created, as required.

s[2:3] := "D"

That expression does not change the existing character of s at index 2, but is equivalent to the expression:

s := s[1:2] || "D" || s[3:0]

Creating a new string by copying existing parts. Internal memory management means that this is a safe thing to do, as many millions of times as an algorithm may need. The heaps will be efficiently managed by the Unicon runtime.

Indexing¶

String indexing positions (or subscripting) is calculated using a cursor that floats “between” characters. Indexing starts at 1, with the virtual cursor positioned before the first character. The end is position “0”, and can count backwards, -1 being the position between the last two characters of the string.

For instance:

"ABC"

That string has positions: 1, 2, 3, 4 (or 0) counting from start to end. Using negative indexing, the positions are: -3, -2, -1, and 0, counting from the end to the start going backwards.

From the end that is

It is important to get used to the idea of position values being before, between and after characters, and that zero is the position past the end of a string.

Pattern¶

Unicon now supports SNOBOL based pattern data.

Regular Expression¶

Along with patterns, Unicon has also added regex literals for string matching. Basic regex at this point.

Non computational types¶

Unicon also supports a variety of non computational types. These vary from File, to Window to other internally managed (usually) non-mutable types.

Note

Unicon does not have pointers, but does manage internal references.

File¶

A value returned from open when using file modes of r, w, a.

Window¶

A graphics context.

Co-expression¶

A very handy code datatype.

Next up, structures¶

Icon and Unicon then add a very nice set of aggregate structures and other high level datatypes. Most of these types are mutable. Slices will be changed in place and not copied as frequently as string data.

From this point on, Icon won’t be mentioned as often, this is a Unicon book.

Index | Previous: Unicon Programming | Next: Data Structures